遗传算法的Matlab实现

本文最后更新于 2025年4月22日 下午

问题描述

我方有一个基地，经度和纬度为（70,40）。假设我方飞机的速度为 1000 公里/小时。我方派一架飞机从基地出发，侦察完敌方所有目标，再返回原来的基地。在敌方每一目标点的侦察时间不计，求该架飞机所花费的时间（假设我方飞机巡航时间可以充分长）。

已知敌方100 个目标的经度、纬度数据在文件sj.txt中

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
53.7121    15.3046    51.1758    0.0322    46.3253    28.2753   30.3313    6.9348
56.5432    21.4188    10.8198    16.2529   22.7891    23.1045   10.1584    12.4819
20.1050    15.4562    1.9451     0.2057    26.4951    22.1221   31.4847    8.9640
26.2418    18.1760    44.0356    13.5401   28.9836    25.9879   38.4722    20.1731
28.2694    29.0011    32.1910    5.8699    36.4863    29.7284   0.9718     28.1477
8.9586     24.6635    16.5618    23.6143   10.5597    15.1178   50.2111    10.2944
8.1519     9.5325     22.1075    18.5569   0.1215     18.8726   48.2077    16.8889
31.9499    17.6309    0.7732     0.4656    47.4134    23.7783   41.8671    3.5667
43.5474    3.9061     53.3524    26.7256   30.8165    13.4595   27.7133    5.0706
23.9222    7.6306     51.9612    22.8511   12.7938    15.7307   4.9568     8.3669
21.5051    24.0909    15.2548    27.2111   6.2070     5.1442    49.2430    16.7044
17.1168    20.0354    34.1688    22.7571   9.4402     3.9200    11.5812    14.5677
52.1181    0.4088     9.5559     11.4219   24.4509    6.5634    26.7213    28.5667
37.5848    16.8474    35.6619    9.9333    24.4654    3.1644    0.7775     6.9576
14.4703    13.6368    19.8660    15.1224   3.1616     4.2428    18.5245    14.3598
58.6849    27.1485    39.5168    16.9371   56.5089    13.7090   52.5211    15.7957
38.4300    8.4648     51.8181    23.0159   8.9983     23.6440   50.1156    23.7816
13.7909    1.9510     34.0574    23.3960   23.0624    8.4319    19.9857    5.7902
40.8801    14.2978    58.8289    14.5229   18.6635    6.7436    52.8423    27.2880
39.9494    29.5114    47.5099    24.0664   10.1121    27.2662   28.7812    27.6659
8.0831     27.6705    9.1556     14.1304   53.7989    0.2199    33.6490    0.3980
1.3496     16.8359    49.9816    6.0828    19.3635    17.6622   36.9545    23.0265
15.7320    19.5697    11.5118    17.3884   44.0398    16.2635   39.7139    28.4203
6.9909     23.1804    38.3392    19.9950   24.6543    19.6057   36.9980    24.3992
4.1591     3.1853     40.1400    20.3030   23.9876    9.4030    41.1084    27.7149

解决方法

使用遗传算法解决如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
% 文件名：example1.m
% 时间：2020年9月13日
% 来源：https://blog.csdn.net/lishan132/article/details/108563593
% 功能：利用遗传算法计算侦察机从基地出发侦查完100个目标耗费的最短时间
clear,close,clc

%数据的读取
load sj.txt        %加载敌方 100 个目标的数据
tic
x=sj(:,1:2:8); x=x(:);
y=sj(:,2:2:8); y=y(:);
sj=[x y]; d1=[70,40];
sj0=[d1;sj;d1]; sj=sj0*pi/180;

%生成距离矩阵
d=zeros(102); %距离矩阵 d
for i=1:101
     for j=i+1:102
         temp=cos(sj(i,1)-sj(j,1))*cos(sj(i,2))*cos(sj(j,2))+sin(sj(i,2))*sin(sj(j,2));
         d(i,j)=6370*acos(temp);
     end
end
d=d+d';

%设置遗传算法参数
L=102;    %编码长度，即个体的基因个数
w=50;     %种群个数，即种群规模
dai=100;  %进化终止代数，程序迭代运行的上限，保证程序有输出

%通过改良圈算法选取优良父代 J
%选取多条较好的路线，一条路线就是一个个体，多个优良个体构成父代J
J = zeros(w,L);
for k=1:w
    c=randperm(100);  %随机置换1到100之间的整数
    c1=[1,c+1,102];   %生成一个初始路线
    flag=1;
    while flag>0
        flag=0;
        for m=1:L-3
            for n=m+2:L-1
                if d(c1(m),c1(n))+d(c1(m+1),c1(n+1))<d(c1(m),c1(m+1))+d(c1(n),c1(n+1))
                    flag=1;
                    c1(m+1:n)=c1(n:-1:m+1);
                end
            end
        end
    end
    J(k,c1)=1:102;
end

%十进制编码，由表现型到基因型的映射，并将每个染色体的值转换为[0,1]之间的浮点数
%本题中，一个种群有50个个体，每一个个体只有1对染色体，每对染色体有102个基因，且1、102号基因固定
J=J/102;    %编码操作
J(:,1)=0;
J(:,102)=1;

%遗传算法实现过程
A=J;   %初始的优良父代A
for k=1:dai   %产生 0～1 间随机数列进行编码
    B=A;
    c=randperm(w);  %随机置换1到w之间的整数
    %交配产生子代 B
    for i=1:2:w
        F=2+floor(100*rand(1)); %生成一个2到101之间的整数（选择一个基因）
        %开始和结束的坐标已经确定，1、102号基因固定，只改变其它基因
        temp=B(c(i),F:102);   %产生交换的基因片段
        B(c(i),F:102)=B(c(i+1),F:102);   %前后两个体交换基因片段
        B(c(i+1),F:102)=temp;            %前后两个体交换基因片段
    end
    %变异产生子代 C
    by=find(rand(1,w)<0.1);     %随机产生变异的个体编号
    if isempty(by)              %没有任何个体发生变异
         by=floor(w*rand(1))+1; %随机选定一个个体发生变异
    end
    C=A(by,:);     %变异产生的新个体
    L3=length(by); %变异的个体数目
    for j=1:L3
        bw=2+floor(100*rand(1,3));   %产生3个随机数，将染色体基因分成4段
        bw=sort(bw);
        C(j,:)=C(j,[1:bw(1)-1,bw(2)+1:bw(3),bw(1):bw(2),bw(3)+1:102]); %交换中间两段的基因片段
    end
    G=[A;B;C]; %经历一代（复制、交叉、变异）后种群的所有个体
    TL=size(G,1);   %当前种群的总个数，即经历一代后种群的规模大小
    %在父代和子代中选择优良品种作为新的父代
    [~,IX]=sort(G,2); %本题中一种巧妙的解码操作，对每一行（每一个个体）的基因进行升排序，IX为的索引号，即完成解码
    temp(1:TL)=0;
    for j=1:TL
        for i=1:101
            %计算每个个体的目标函数值（侦查总距离）
            temp(j)=temp(j)+d(IX(j,i),IX(j,i+1));
        end
    end
    [DZ,IZ]=sort(temp);  %按目标函数值递增排序
    A=G(IZ(1:w),:);      %选取目标函数值较小（适应度值高）的前50个个体，作为下一代的个体
end

%生成最佳路径（最佳个体）及距离（目标函数值）
path=IX(IZ(1),:);  %选择最后一代群体中的最优个体（适应度最高，侦查总距离最小）
long=DZ(1);        %最优个体的目标函数值（侦查距离）

%输出结果
fprintf('侦查耗费总时间:%.2f小时\n',long/1000)
toc

%绘制坐标图
plot(x,y,'bO')      %目标坐标
hold on
plot(70,40,'p',...  %基地坐标
    'MarkerSize',10,...
    'MarkerEdgeColor','b',...
    'MarkerFaceColor','r')
hold on
%绘制侦查路线图
xx=sj0(path,1);
yy=sj0(path,2);
plot(xx,yy,'-r')
%绘图说明
xlabel("经度")
ylabel("纬度")
title("侦查示意图")
legend("侦查目标","我方基地","侦查路线")

运行结果

遗传算法每次运行的结果都不一样，下面选了一次效果比较好的结果展示

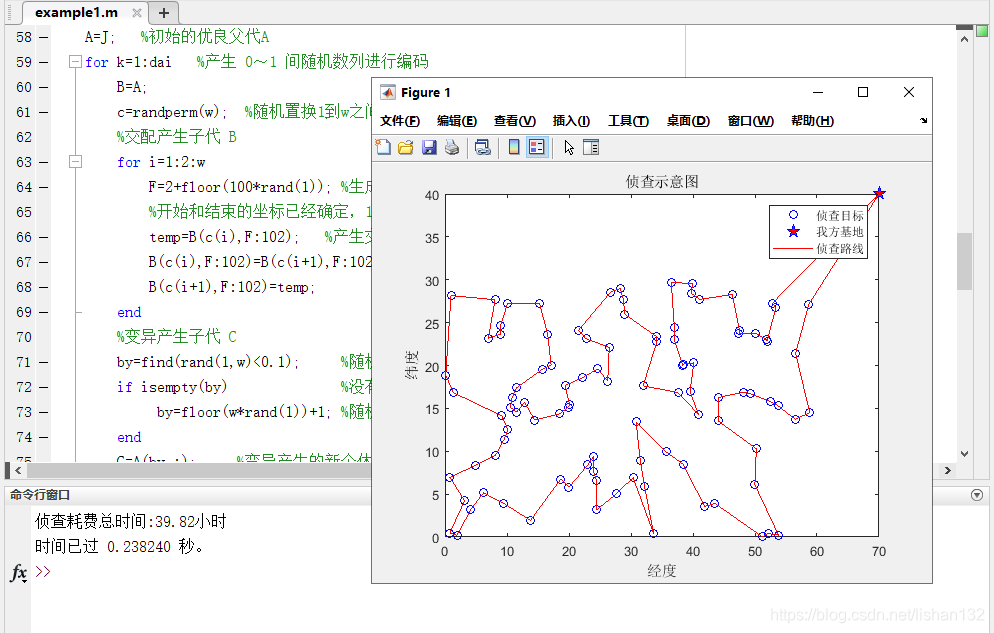
结论

本文根据已有的资料，对遗传算法的Matlab程序进行分析，完善，并添加了相应的注释，给出了解决目标侦查路线问题，其本质也是TSP（Travelling salesman problem）问题的解决过程。

遗传算法的核心是三种遗传算子（复制、交叉、变异）的遗传策略以及最优个体的选择策略，更改程序中相应的参数，可以解决类似的组合优化问题。

文中核心代码源自网上资料，名为《数模大全》的第二十三章现代优化算法，但书名、作者均无法考证，但作者做了一些适应性的修改。

本文程序的特点说明：

  1. 程序中的交叉概率、变异概率均为随机生成，每一次迭代都不一样；
  2. 交叉策略为断点交叉，即选择一个断点，断点右端的染色体全部交换；
  3. 染色体编码方式为浮点数编码；选择最优个体的方式是简单的排序选择，目标函数值越小，适应度值越大；
  4. 程序终止的唯一条件是达到最终迭代次数。

本文程序后续的改进方向：

  1. 更改交叉概率、变异概率产生的方式，如设置一个不变的常数
  2. 更改编码、解码的方式，如二进制编码
  3. 更改交叉、变异的方式，如单点交叉、两点交叉、多点交叉、均匀交叉、位变异、均匀变异、倒位操作等
  4. 更改选择最优个体的方式，如轮盘赌法、两两竞争法等
算法实现
#Matlab编程
遗传算法的Matlab实现
https://www.bit01.top/2025/03/25/matlab-genetic-algorithm/
作者
李珊
发布于
2025年3月25日
更新于
2025年4月22日
许可协议