蒙特卡洛加模拟退火算法的Matlab实现

本文最后更新于 2025年4月22日 下午

问题描述

  1. 一个企业生产一件产品共有M项任务需要完成，依次记为A、B、C、……
  2. 任务的完成需要遵循一定的顺序，A任务完成后才能去完成B，B完成后才能去完成C，以此类推，称为有顺序约束。
  3. 此时有N(N>=M)名员工可以完成这些任务，员工编号依次为1、2、3….，且每个员工只能固定完成一项任务
  4. 由于工作能力不同，每名员工完成不同任务耗费的时间不一样，如下表1所示。
任务/时间 1 2 3 4 5
A 21 18 16 22 14
B 35 28 33 26 22
C 12 16 11 14 11

  1. 现按任务的顺序为各任务安排合适的员工，各员工按编号从小到大的顺序进行排队，对每一个员工可以做出同意或拒绝的选择，且只有一次机会，当选择同意时，按任务的先后顺序为此员工安排一项任务，当选择拒绝时，此员工离开队伍，后续不能再向其安排任务。例如：

    • 当前最新任务为A，1号员工到来，拒绝1号完成任务A，1号离开，2号员工到来，接受2号员工完成任务A

    • 当前最新任务变为B，3号员工到来，拒绝3号完成任务B，3号离开，4号员工到来，接受4号员工完成任务B

    • 当前最新任务变为C，5号员工到来，接受5号员工完成任务C

因为条件5的限制，导致表1发生了一些变化，

  • 1号员工不可能分配到任务B、C、…，因为这样就没有员工完成A了，同理有以下限制
  • 2号员工不可能分配到任务C…
  • 4号员工不可能分配到任务A…
  • 5号员工不可能分配到任务A、B…

对于不可能分配到的任务，此员工完成时间记为无穷大，如下表2所示

任务/时间 1 2 3 4 5
A 21 18 16 ∞ ∞
B ∞ 28 33 26 ∞
C ∞ ∞ 11 14 11

问此时如何为每一个任务分配一个员工去，能够达到生产一件产品耗费总时间最小？

分析问题

理想情况下，应该为每一个任务安排耗时最短的员工完成，可以看到，3号员工完成任务A，4号员工完成任务B，5号员工完成任务C，刚好满足条件，而且完美错开，可以达到总耗时最短的要求，总耗时为16+26+11=53。但是如果错不开怎么办，即某一个员工在完成多件任务都是耗时最短的情况下，就不能这么简单处理了，所以要考虑一般的情况。

一般的，在这个问题中，任务的完成是固定顺序，员工的选择也是从前到后，那么组合的情况就是123、124、134、235等等。可以认为是从5个员工中选3个，然后按顺序排队，依次分配一个任务，可以选择的组合数为$C^3_5$对每一种组合下计算对应的耗费时间，即可得到耗时最短的一种组合情况。

Matlab程序如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
% 文件名：example1.m
% 时间：2020年9月29日
% 作者：乐观的lishan
% 功能：遍历法计算顺序指派问题
clear,close,clc
warning off
tic

%生成代价矩阵
d = [21   18   16   inf   inf;
     inf  28   33   26    inf;
     inf  inf  11   14    11];

M = size(d,1);    %任务数
N = size(d,2);    %员工数,员工应数大于或等于任务数

C = nchoosek(1:N,M);  %求出所有的组合情况
n = size(C,1);
Sum = zeros(n,1);
for i = 1:n
    for j = 1:M
         Sum(i) = Sum(i) + d(j,C(i,j));
    end

end
min_Sum = min(Sum);
min_plan = (C((Sum == min_Sum),:));
num_plan = size(min_plan,1);
toc

%输出结果
fprintf('完成指派任务的方案总数为:%.0f\n',n)
fprintf('完成指派任务耗费的最短时间为:%.0f\n',min(Sum))
for i = 1:num_plan
    fprintf('对应第%d种指派方案为:%s\n',i,num2str(min_plan(i,:)))
end
%绘制耗费时间坐标图
plot(Sum,'r','LineWidth',2)
%绘图说明
xlabel('组合编号')
ylabel('耗费时间')
title('不同组合方案下的时间耗费示意图')

求出结果如下：

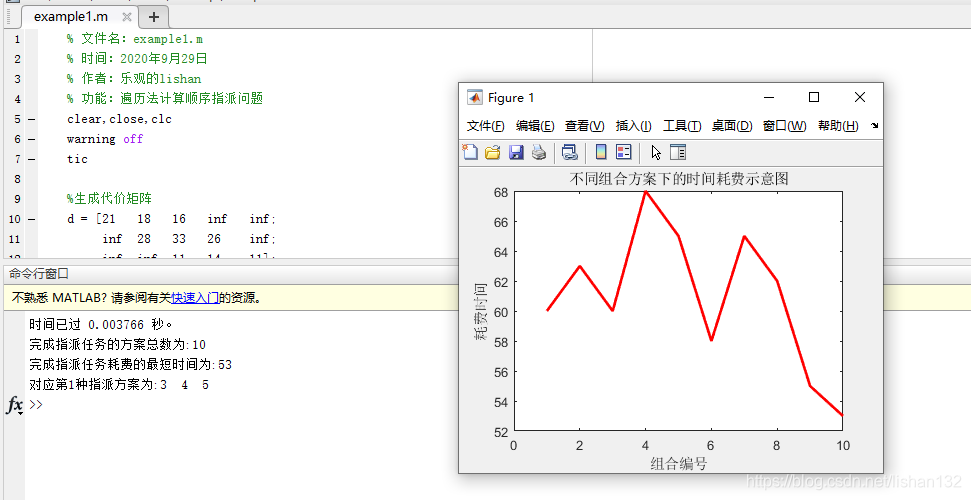
求出结果为3号员工完成任务A，4号员工完成任务B，5号员工完成任务C，此时耗费时间最短，最短时间为53

但是这是数据量比较少的情况，一旦数据增大，就不能再使用遍历了，比如，任务数为27，员工数为35，组合方式就达两千三百万种之多，此时需要寻找一种更好的方法

解决方法

更一般的，对于一个离散的组合优化问题，可以使用蒙特卡洛加模拟退火算法解决

算法步骤描述如下：

  • step1：使用蒙特卡洛方法生成随机选择一个最优的组合，作为初始解，并计算初始能量值（目标函数值）

  • step2：初始化模拟退火算法参数，初始温度T，终止温度e，温度衰减因子alf，马尔科夫链长度L，能量不再降低的次数上限cnt_limit

  • step3：马尔科夫链长度加1，判断是否达到上限，若是，算法结束，否则，开始step4

  • step4：当前温度下，在当前解的基础上进行扰动构造一个新解，本文中构造方法为：先将当前解的组合中随机去掉一个员工，再随机添加一个新员工。生成一个新解（一种组合），并计算能量值，即目标函数值（耗费总时间）

  • step5：计算与前一个解的能量之差

  • step6：根据能量差判断是否接受新解。若能量差小于0 ，说明新解的能量更低，接受新解；否则 ，说明新解的能量没有下降，以玻尔兹曼概率接受新解。同时记录最优解和对应的最低能量值（最小目标函数值）

  • step7：判断最低能量值是否保持不变，若是，计数器加1，否则，计数器清0。若计数器到达上限，算法结束。

  • step8：降低温度，判断温度是否达到下限，若是，算法结束，否则，转向step3

程序如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
% 文件名：example2.m
% 时间：2020年9月29日
% 作者：乐观的lishan
% 功能：利用模拟退火算法计算有顺序约束的指派问题
clear,close,clc
warning off
tic

%数据的生成
M = 27;       %任务数
N = 35;       %员工数,员工应数大于任务数
lb = 10;      %成本下限
ub = 35;      %成本上限

%利用随机数生成代价矩阵
d = unifrnd (lb, ub, M, N);  %生成一个服从均匀分布的矩阵，数值范围[lb,ub]，矩阵大小M×N
d = ceil(d); %朝正无穷大取整
for i = 2:M
    d(i,1:i-1) = inf;
    d(M-i+1,N-(i-1)+1:N) = inf;
end

% 保存数据，可用于下一次用相同的数据实验
save data

%运行一次后可将此行上面的所有代码注释，再次运行即可使用相同的数据
load data.mat

%初始化决策变量和函数值，即模拟退火中的状态和内能
S0 = sort(randperm(N,M));    %初始化分配策略，决策变量，即状态
Sum = inf;                   %初始化能量，目标函数值
H = 20;                      %蒙特卡洛生成组合数次数
%生成初始解，用蒙特卡洛方法随机生成H种组合，并选择其中一个较好的指派组合
for j = 1:H
     S = sort(randperm(N,M));
     temp = 0;
     for i = 1:M
         temp=temp+d(i,S(i));
     end
     if temp < Sum
         S0 = S;
         Sum = temp;
     end
end
%记录蒙特卡洛选优结果
sum = Sum;
s0 = S0;

%模拟退火算法的参数设置
e = 0.1^30; %终止温度
L = 5000;    %Markov链长度
alf = 0.999; %温度衰减因子
T = 1;       %起始温度
cnt_limit = 300;        %最优值连续保持不变的次数上限

all_people = 1:N;       %所有元素构成的集合
S0 = s0;
cnt = 0;

record_solve(1,:) = S0;
record_value(1,:) = 0;
for i = 1:M
    record_value = record_value + d(i,S0(i));
end

%退火过程
for k=2:L
    %产生新解
    original_solve = S0; %保留原解
    remain_people = setdiff(all_people,S0);    %求当前解在所有元素构成的集合中的补集
    index1 = randperm(N-M,1);
    index2 = randperm(M,1);
    add_num = remain_people(index1);   %随机添加一个新元素
    S0(index2) = [];                   %随机删除当前解的一个元素
    new_solve = sort([S0,add_num]);    %添加一个新元素并排序生成新解
    record_solve(k,:) = new_solve;
    %计算代价函数值，即当前时刻目标值（内能）减去前一时刻目标值（内能）
    d1 = 0;
    d2 = 0;
    for i = 1:M
        d1 = d1 + d(i,original_solve(i));        %交换前，目标函数值
        d2 = d2 + d(i,new_solve(i));             %交换后，目标函数值
    end
    df = d2-d1; %内能差
    record_value(k,:) = d2;

    %接受准则
    if df<0  %内能降低，此解与上一解比较更优
        S0 = new_solve;
        if d2 < Sum(k-1)
            bset_solve = new_solve;
            Sum(k) = d2;
        else
            Sum(k) = Sum(k-1);
        end
    else
        if exp(-df/T)>rand(1)  %内能增大，此解与上一解比较更差，以玻尔兹曼概率接受此解
            S0 = new_solve;
        else    %内能增大，且不接受新解
            S0 = original_solve;
        end
        Sum(k) = Sum(k-1);
    end

    %判断最优值是否不再变动
    if Sum(k) == Sum(k-1)
        cnt = cnt + 1;
        if cnt >= cnt_limit
            break;
        end
    else
        cnt = 0;
    end

    %温度判断
    T=T*alf;  %降低温度，开始冷却
    if T<e   %温度小于临界值，算法提前结束
        break;
    end
end

toc

%结果验证
d3 = 0;
for i = 1:M
    d3 = d3 + d(i,bset_solve(i));
end
if d3 == Sum(end)
    fprintf('结果验证【成功】\n')
else
    fprintf('结果验证【失败】\n')
end

best_plan = (record_solve((record_value == Sum(end)),:));
[b,location]= unique(best_plan,'rows','first');
res = sortrows([location,b]);
new_best_plan=res(:,2:size(res,2));
%输出结果
fprintf('完成指派任务的方案总数为:%.0f\n',nchoosek(N,M))
fprintf('程序迭代次数为:%.0f\n',length(Sum))
fprintf('完成指派任务所需的最少成本为:%.0f\n',Sum(end))
for i = 1:size(new_best_plan,1)
    fprintf('对应第%d种指派方案为:%s\n',i,num2str(new_best_plan(i,:)))
end

%绘制收敛坐标图
plot(Sum,'r','LineWidth',2)
%绘图说明
xlabel('收敛次数')
ylabel('成本值')
title(['收敛示意图：','第',num2str(length(Sum)),'次收敛'])

运行结果

记录两次较好的运行结果

运行结果1：

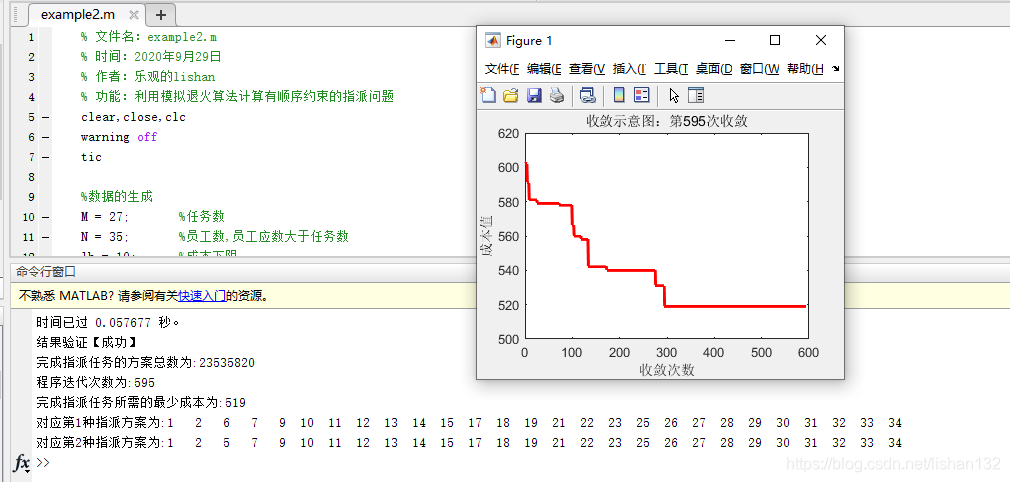
运行结果2：

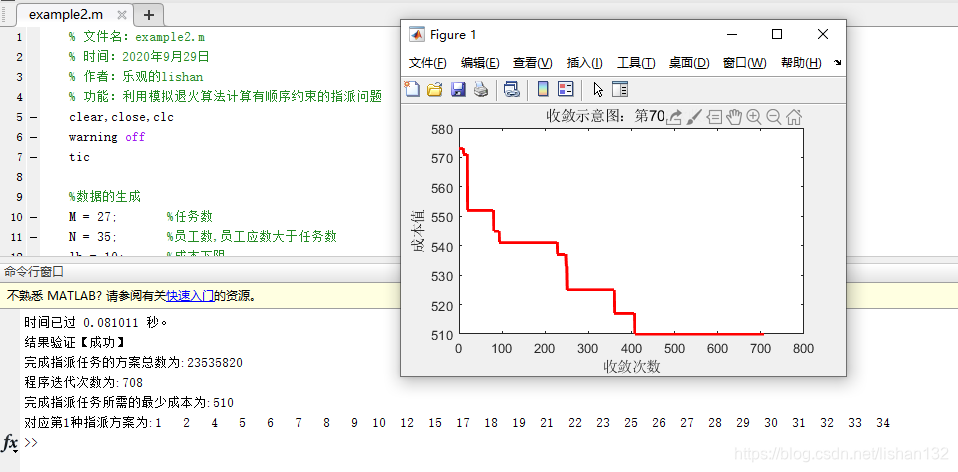
更改任务数、员工总数，程序也能很快的完成收敛。当然模拟退火每次运行结果不一样，可以多运行几次，记录一个较好的结果，这样能够在短时间内得到一个较好解方案。通过遍历法可以验证模拟退火算法结果的有效性，其结果保持一致，但模拟退火算法可以更快得出结果。

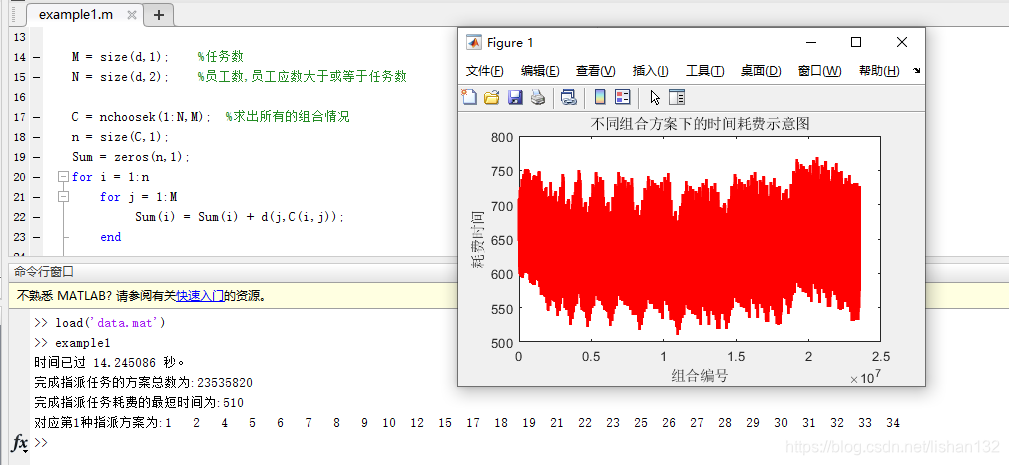
结论

本文首先对有顺序约束的任务指派问题进行了分析，有顺序约束即任务的完成有先后顺序之分，员工的选取也有先后顺序之分，即只能向后选取，在这个限制条件下，本文先给出了遍历法的解决方法，并给出了Matlab代码和示例结果；然后再提出在任务数和员工数增大的情况下遍历法不再适用，因为本质上这是一个离散的组合优化问题，由此引入了蒙特卡洛算法加模拟退火算法的解决思路，并给出了算法步骤和Matlab代码以及示例结果。

本文的模拟退火算法与一般退火算法不同，由于本文的组合情况有顺序约束，常规退火算法中的扰动方法不再适用，本文使用方法为：在当前解中随机删除一个元素，再随机加入一个新元素的方法构造新解，最终取得了比较好的效果。

感谢博主“乐观的阿锡”乐观的阿锡的博客_CSDN博客-计算机,go语言,Linux系统编程学习笔记领域博主为本文提供了问题基础以及解决的思路

参考

  • [1] 李冰,徐杰,杜文.用模拟退火算法求解有顺序约束指派问题[J].系统工程理论方法应用,2002(04):330-335.

  • [2] 赵越.模拟退火算法求解指派问题新探[J].吉林建筑工程学院学报,2011,28(04):61-63.

算法实现
#Matlab编程
蒙特卡洛加模拟退火算法的Matlab实现
https://www.bit01.top/2025/03/25/matlab-montecarlo-simulated-annealing-algorithm/
作者
李珊
发布于
2025年3月25日
更新于
2025年4月22日
许可协议