模拟退火算法的Matlab实现

本文最后更新于 2025年4月22日 下午

问题描述

我方有一个基地，经度和纬度为（70,40）。假设我方飞机的速度为 1000 公里/小时。我方派一架飞机从基地出发，侦察完敌方所有目标，再返回原来的基地。在敌方每一目标点的侦察时间不计，求该架飞机所花费的时间（假设我方飞机巡航时间可以充分长）。

已知敌方100 个目标的经度、纬度数据在文件sj.txt中

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
53.7121    15.3046    51.1758    0.0322    46.3253    28.2753   30.3313    6.9348
56.5432    21.4188    10.8198    16.2529   22.7891    23.1045   10.1584    12.4819
20.1050    15.4562    1.9451     0.2057    26.4951    22.1221   31.4847    8.9640
26.2418    18.1760    44.0356    13.5401   28.9836    25.9879   38.4722    20.1731
28.2694    29.0011    32.1910    5.8699    36.4863    29.7284   0.9718     28.1477
8.9586     24.6635    16.5618    23.6143   10.5597    15.1178   50.2111    10.2944
8.1519     9.5325     22.1075    18.5569   0.1215     18.8726   48.2077    16.8889
31.9499    17.6309    0.7732     0.4656    47.4134    23.7783   41.8671    3.5667
43.5474    3.9061     53.3524    26.7256   30.8165    13.4595   27.7133    5.0706
23.9222    7.6306     51.9612    22.8511   12.7938    15.7307   4.9568     8.3669
21.5051    24.0909    15.2548    27.2111   6.2070     5.1442    49.2430    16.7044
17.1168    20.0354    34.1688    22.7571   9.4402     3.9200    11.5812    14.5677
52.1181    0.4088     9.5559     11.4219   24.4509    6.5634    26.7213    28.5667
37.5848    16.8474    35.6619    9.9333    24.4654    3.1644    0.7775     6.9576
14.4703    13.6368    19.8660    15.1224   3.1616     4.2428    18.5245    14.3598
58.6849    27.1485    39.5168    16.9371   56.5089    13.7090   52.5211    15.7957
38.4300    8.4648     51.8181    23.0159   8.9983     23.6440   50.1156    23.7816
13.7909    1.9510     34.0574    23.3960   23.0624    8.4319    19.9857    5.7902
40.8801    14.2978    58.8289    14.5229   18.6635    6.7436    52.8423    27.2880
39.9494    29.5114    47.5099    24.0664   10.1121    27.2662   28.7812    27.6659
8.0831     27.6705    9.1556     14.1304   53.7989    0.2199    33.6490    0.3980
1.3496     16.8359    49.9816    6.0828    19.3635    17.6622   36.9545    23.0265
15.7320    19.5697    11.5118    17.3884   44.0398    16.2635   39.7139    28.4203
6.9909     23.1804    38.3392    19.9950   24.6543    19.6057   36.9980    24.3992
4.1591     3.1853     40.1400    20.3030   23.9876    9.4030    41.1084    27.7149

解决方法

使用模拟退火算法解决如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
% 文件名：example1.m
% 时间：2020年9月13日
% 来源：https://blog.csdn.net/lishan132/article/details/108559016
% 功能：利用模拟退火算法计算侦察机从基地出发侦查完100个目标耗费的最短时间
clc,close,clear

%数据的读取
load sj.txt     %加载敌方 100 个目标的数据，数据按照表格中的位置保存在纯文本文件 sj.txt 中
tic
x=sj(:,1:2:8);x=x(:);
y=sj(:,2:2:8);y=y(:);
sj=[x y]; d1=[70,40];
sj=[d1;sj;d1]; sj=sj*pi/180;

%%生成距离矩阵
d=zeros(102);
for i=1:101
     for j=i+1:102
         temp=cos(sj(i,1)-sj(j,1))*cos(sj(i,2))*cos(sj(j,2))+sin(sj(i,2))*sin(sj(j,2));
         d(i,j)=6370*acos(temp);
     end
end
d=d+d';

%初始化决策变量和函数值，即模拟退火中的状态和内能
S0=[];    %初始化路线，决策变量，即状态
Sum=inf;  %初始化侦查距离，目标函数值

%生成初始解，用蒙特卡洛方法随机生成一个较好的路线组合
%100个目标点，理论上有100!=9.3326e+157种组合，此问题属于NP难题
for j=1:1000
     S=[1 1+randperm(100),102];
     temp=0;
     for i=1:101
         temp=temp+d(S(i),S(i+1));
     end
     if temp<Sum
         S0=S;
         Sum=temp;
     end
end

%模拟退火算法的参数设置
e=0.1^30; %终止温度
L=50000;  %Markov链长度
at=0.999; %温度衰减因子
T=1;      %起始温度

%退火过程
for k=1:L
    %两交换法产生新解
    c=2+floor(100*rand(1,2)); %随机生成2个整数，范围[2,101]
    c=sort(c);  %从小到大排序
    c1=c(1);
    c2=c(2);
    %交换两个点之间的访问顺序，计算代价函数值，即当前时刻目标值（内能）减去前一时刻目标值（内能）
    %交换如下（本示例中侦查目标坐标编号为2,3,4....101）：
    %交换前访问顺序：...-5-6-31-  c1-21-12-52-c2  -87-63-....
    %交换后访问顺序：...-5-6-31-  c2-52-12-21-c1  -87-63-....
    d1 = d(S0(c1-1),S0(c1))+d(S0(c2),S0(c2+1)); %交换前，31-c1距离加上c2-87的距离
    d2 = d(S0(c1-1),S0(c2))+d(S0(c1),S0(c2+1)); %交换后，31-c2距离加上c1-87的距离
    df = d2-d1;
    %接受准则
    if df<0  %内能降低，此解与上一解比较更优
        S0=[S0(1:c1-1),S0(c2:-1:c1),S0(c2+1:102)];
        Sum=Sum+df;
    elseif exp(-df/T)>rand(1)  %内能增大，此解与上一解比较更差，以玻尔兹曼概率接受此解
        S0=[S0(1:c1-1),S0(c2:-1:c1),S0(c2+1:102)];
        Sum=Sum+df;
    end
    T=T*at;  %降低温度，开始冷却
    if T<e   %温度小于临界值，算法提前结束
        break;
    end
end
toc
%输出结果
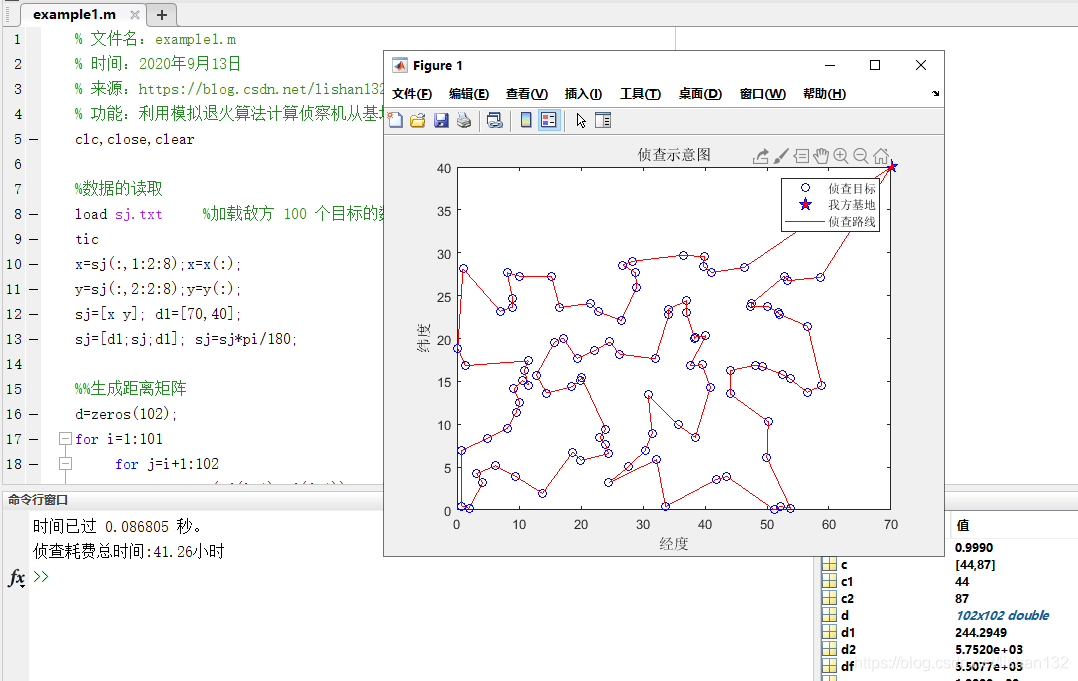
fprintf('侦查耗费总时间:%.2f小时\n',Sum/1000)

%绘制坐标图
 plot(x,y,'bO')      %目标坐标
 hold on
 plot(70,40,'p',...  %基地坐标
    'MarkerSize',10,...
    'MarkerEdgeColor','b',...
    'MarkerFaceColor','r')
 hold on
 %绘制侦查路线图
 plot([x(S0(2)-1),70,x(S0(101)-1)],[y(S0(2)-1),40,y(S0(101)-1)],'-r')
 for i = 1:99
    plot([x(S0(i+1)-1),x(S0(i+2)-1)],[y(S0(i+1)-1),y(S0(i+2)-1)],'-r')
 end
 %绘图说明
 xlabel("经度")
 ylabel("纬度")
 title("侦查示意图")
 legend("侦查目标","我方基地","侦查路线")

运行结果

退火算法每次运行的结果都不一样，下面选了一次效果比较好的结果展示

结论

本文根据已有的资料，对模拟算法的Matlab程序进行分析，完善，并添加了相应的注释，给出了解决目标侦查路线问题，其本质也是TSP（Travelling salesman problem）问题的解决过程。

模拟退火的核心是构造新解的方法、以及设计接受新解的策略，通过设置温度参数可以控制模拟退火算法的运行过程。

文中核心代码源自网上资料，名为《数模大全》的第二十三章现代优化算法，但书名、作者均无法考证，但作者做了一些适应性的修改。

算法实现
#Matlab编程
模拟退火算法的Matlab实现
https://www.bit01.top/2025/03/25/matlab-simulated-annealing-algorithm/
作者
李珊
发布于
2025年3月25日
更新于
2025年4月22日
许可协议