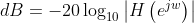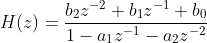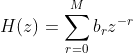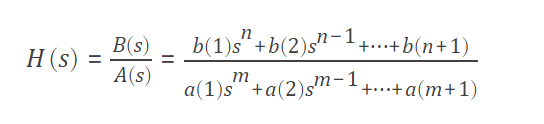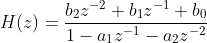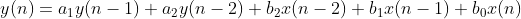本文最后更新于 2025年5月21日 下午
0 前言 本文是作者在做数字信号处理作业时对Matlab下设计数字滤波器的一些总结,给出了普遍使用的数字滤波器代码,修改参数即可移植使用。文中如有错误,欢迎留言批评、指正。
1 数字滤波器的设计方法概述 滤波器特性介绍 :滤波器的作用就是过滤波形,这里的滤波不是指在时间上截取某一部分波形,而是指过滤掉不需要的波形成分,即只让需要的波形成分通过,不需要的波形就被抛弃了。波形成分一般用频率(Hz)来描述,也可以用模拟角频率(rad/s)和数字角频率(rad)来描述。一个理想的滤波器的特性就是只允许将某个要求频带范围内的波形成分全部通过,比如将500Hz到1000Hz之间的波形成分全部一个不少的输出,并且其形状不能发生任何改变,也就是说原来波形的相位可以左右平移,但是幅度大小不能改变,对于小于500Hz和大于1000Hz的波形来说,就一点儿成分也不能输出,幅度大小为0。理想的滤波器是不可能实现的,但是我们可以无限逼近这一特性,这就需要对设计的滤波器进行性能指标描述。
可实现的滤波器 :理想的滤波器严格的将某个频率点两端的成分分开,这个频率点被称为截止频率Wc,截止频率的一端允许通过(即幅度保持不变),另一端不允许通过(即幅度全部为0)。实际上做不到这一点,但放宽要求可以实现,在截止频率点向左、右分别移动一定距离,可以确定两个新的频率点,这两个新的频率点之间的频率成分就是过渡带。把这两个新的频率点分别称为通带截止频率(fp或Wp)和阻带截止频率(fs或Ws)。同样,波形的幅度也不能保证全部保持恒定不变,在通带范围内的幅度衰减称为通带衰减大小,在阻带范围内的幅度衰减称为阻带衰减大小,幅度的衰减大小一般用分贝(dB)表示。假如过渡带中的频率成分幅度缓慢衰减是可以接受的(过渡带中幅度的衰减一般是单调下降的),通带和阻带的幅度在一定范围内发生起伏波动(也叫纹波)也是可以接受的,那么就可以实现这样的滤波器。
滤波器的分类 :从滤波器的通带范围来可将滤波器分为低通、高通、带通、带阻滤波器;从滤波器可以处理的输入信号来看可滤波器分为模拟滤波器和数字滤波器;实际运用中,模拟滤波器在物理上可用电阻、电容等元件搭建电路实现,数字滤波器一般通过处理器用算法实现。本文重点介绍在Matlab下的数字滤波器仿真设计。
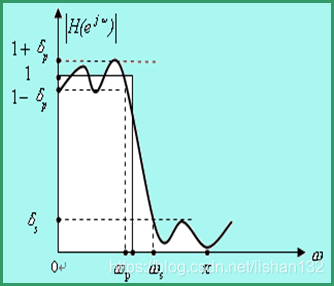
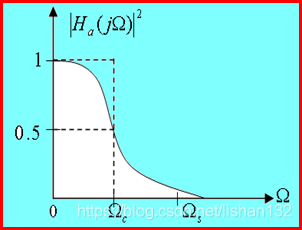
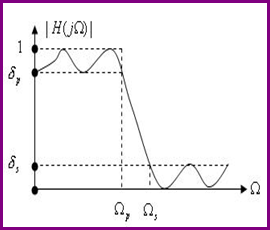
下图描述了一个可实现的低通滤波器的幅频特性曲线图,其中矩形部分表示理想滤波器,曲线部分表示实际的滤波器,Wp表示通带截止频率,Ws表示阻带截止频率,Wp和Ws之间还有一个频率点,这就是矩形代表的理想滤波器的截止频率。在实际滤波器中,截止频率处的幅度衰减定义为3dB,也就是幅度衰减到原来的0.707,功率衰减到原来的0.5左右。δF和δs分别被称为通带衰减大小和阻带衰减大小。
一个可实现的低通滤波器幅频特性曲线如下
备注 :频率(f)、模拟角频率(Ω)、数字角频率(w)之间的换算:Ω=2πf,w=ΩT,w=Ω/Fs,其中,T为对模拟信号的采样周期,Fs为采样频率。分贝dB和幅度值之间的换算如下:
1、确定滤波器性能指标
通带误差:包括通带截止频率、通带最大衰减分贝
阻带误差:包括阻带截止频率、阻带最小衰减分贝
过渡带:通带截止频率与阻带截止频率之差
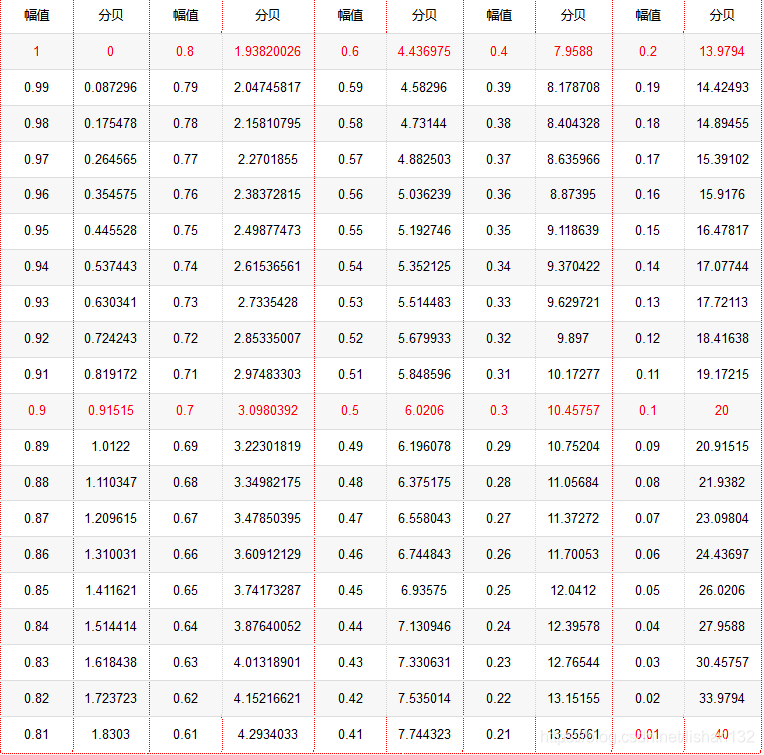
比如:要求设计一个低通滤波器,截止频率为2000Hz,即理想上要求把0~2000Hz之间的波形成分全部不改变形状的输出。为了接近这一特性,通带截止频率设置为1900Hz,通带衰减不大于3dB(0.707),阻带截止频率设置为2200Hz,阻带衰减不小于40dB(0.01),下表给出了归一化幅值与分贝之间的转换表,归一化幅值表示衰减到原来幅值的比例,或者说衰减到原来的百分比,比如40dB表示衰减到原来的0.01,也就是1%。性能指标的选择范围不一样,实现滤波器的复杂度、成本以及最终的效果都是不一样的,这需要根据实际情况进行平衡选择。当然,如果仅仅是在Matlab下做仿真,就不需要考虑复杂度和成本等因素了。
归一化幅值转分贝图如下所示:
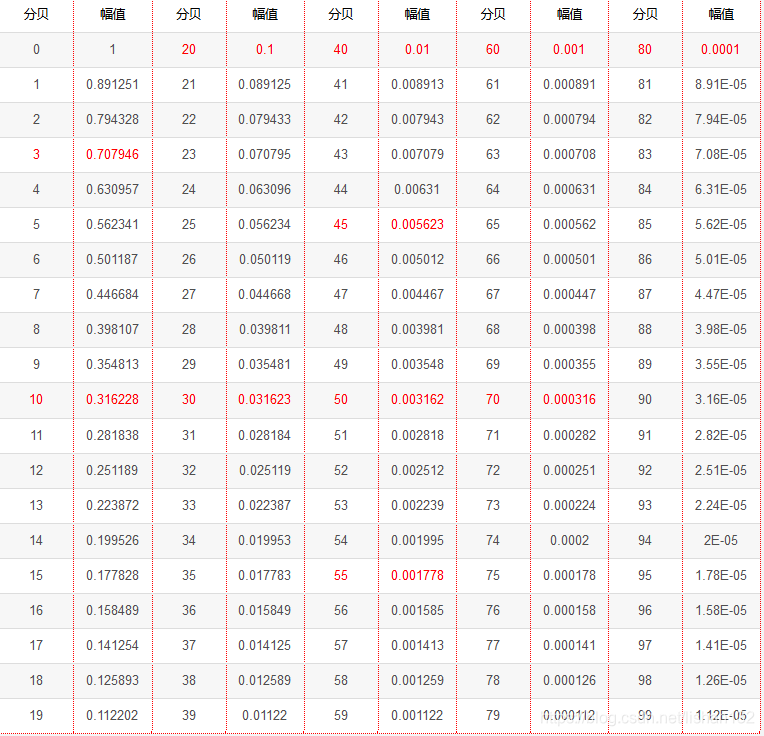
分贝转归一化幅值图如下所示:
2、数字滤波器的分类
设计数字滤波器本质上说就是设计一个因果稳定系统,一个离散的数字信号通过这个系统后,数字滤波器系统可以输出期望的频率成分。按数学滤波器系统的单位取样响应可将数字滤波器分为IIR和FIR两大类。
IIR:无限冲激响应系统,可以用有理分式表示系统函数。简单理解就是存在分母表达式
特点:IIR滤波器设计方法简单,阶次低,运算量小,经济高效,幅频特性较好,但是必须考虑极点对系统稳定性的影响,即分母不能为0,这是使得系统函数有意义的前提。同时,相频特性存在一定程度的失真。适合用于对相位要求不高的场合,如信号检测、语音通信等,这些场合更看重信号的幅度大小。
FIR:有限冲激响应响应系统,可以用有理多项式表示系统函数。简单理解就是不存在分母,FIR是IIR的一种特例,即参数a向量的值全部取0。
特点:FIR与IIR刚好相反,FIR滤波器不存在极点,不需要考虑极点对系统稳定性的影响。同时,可以采用快速傅里叶变换算法实现快速卷积(因为符合傅里叶变换公式的形式),在相同阶次下,运算速度更快。但是设计会更复杂,相同的频率特性下,其阶次也比IIR要高,运算量大,成本高。主要适用于对相位要求较高的场合,如图像处理等,这种场合下,相位稍有偏移,图片就变得模糊,对幅度的大小要求反而不高。
2 IIR数字滤波器的设计方法 2.1 模拟滤波器设计 先设计出一个模拟滤波器,再对这个模拟滤波器的系统函数进行离散周期采样就可得到数字滤波器的系统函数,在实际中普遍使用冲击响应不变法 或双线性映射法 将模拟滤波器转换为数字滤波器。这里的模拟滤波器通常被称为原型滤波器,最著名的是巴特沃斯滤波器、切比雪夫滤波器和椭圆滤波器,对这三种经典滤波器Matlab都有库函数可以调用。
2.1.1 巴特沃斯滤波器设计 巴特沃斯滤波器幅频特性曲线如下:
巴特沃斯滤波器函数介绍:
在Matlab命令窗口输入doc buttord 和doc butter 即可查看详情
1、buttord函数 :生成巴特沃斯滤波器的阶次N和截止频率Wc
截止频率Wc:幅度响应衰减为为原来的0.707时的频率点,衰减大小为3dB
阶次N:阶次越高,在截止频率两侧衰减越快,滤波器越复杂,成本越高
[N,Wc]=buttord(Wp,Ws,Rp,Rs,’s’);有参数‘s’时,表示生成巴特沃斯模拟滤波器的参数,此时,Wp、Ws和Wc表示模拟角频率
2、butter函数 :设计巴特沃斯滤波器
[b,a] = butter(N,Wc,’low’,’s’);有参数‘s’时,返回N阶低通模拟巴特沃斯滤波器的传递函数系数,b为系统函数分子系数,a为系统函数分母系数,Wc为截止模拟角频率
其中的‘low’可以替换成’bandpass’、’high’、’stop’,分别表示带通、高通、带阻滤波器
3、freqs函数:模拟滤波器的频率响应
[h,w] = freqs(b,a,n);计算频率模拟滤波器的频率响应,b为系统函数分子系数,a为系统函数分母系数,n为频率点数,如果不指定n,n取默认值200
Matlab程序设计如下:
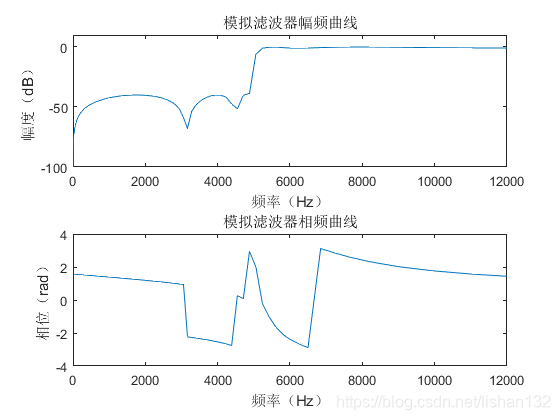
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 1 ;switch filter_typecase 1 1900 ;fs=2200 ;case 2 5100 ;fs=4700 ;case 3 1100 ,1900 ];fs=[900 ,2100 ];case 4 900 ,2100 ];fs=[1100 ,1900 ];end 1 ;Rs=40 ;2 *pi *fp;Ws=2 *pi *fs; 's' );switch filter_typecase 1 'low' ,'s' );case 2 'high' ,'s' );case 3 'bandpass' ,'s' );case 4 'stop' ,'s' );end abs (H);angle (H);20 *log10 ((mag+eps )/max (mag));2 *pi );2 ,1 ,1 );plot (f,db);'模拟滤波器幅频曲线' );xlabel('频率(Hz)' );ylabel('幅度(dB)' );2 ,1 ,2 );plot (f,pha);'模拟滤波器相频曲线' );xlabel('频率(Hz)' );ylabel('相位(rad)' );
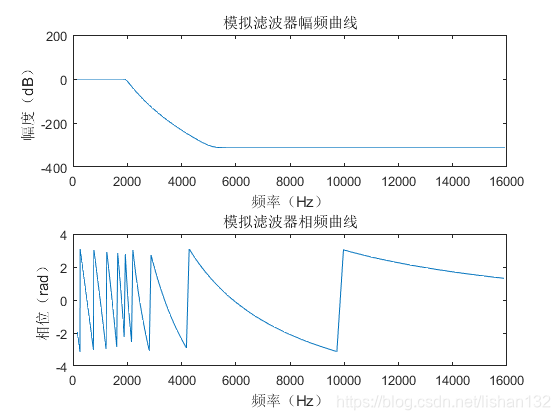
模拟低通巴特沃斯滤波器设计效果如下:
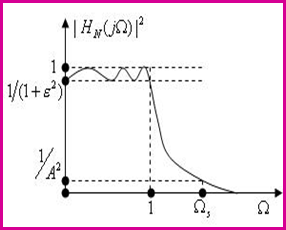
2.1.2 切比雪夫滤波器设计 切比雪夫1型滤波器幅频特性如下
切比雪夫有两种类型,类型1只在通带有纹波起伏,类型2只在阻带有纹波起伏,其程序设计完全一样,只需要将主要函数名及相应参数更改即可,值得注意的是,cheby1的参数有通带衰减大小Rp,cheby2的参数有阻带衰减大小Rs,
切比雪夫1型模拟滤波器
1、cheb1ord函数
[N,Wc]=cheb1ord(Wp,Ws,Rp,Rs,’s’);%计算切比雪夫1模拟滤波器参数,‘s’表示Wp和Ws都是模拟角频率
2、cheby1函数
[b,a]=cheby1(N,Rp,Wp,’low’,’s’);%设计切比雪夫1低通滤波器,其中的‘low’可以替换成’bandpass’、’high’、’stop’,分别表示带通、高通、带阻滤波器
切比雪夫1型模拟滤波器Matlab程序设计如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 1 ;switch filter_typecase 1 1900 ;fs=2200 ;case 2 5100 ;fs=4800 ;case 3 1100 ,1900 ];fs=[900 ,2100 ];case 4 900 ,2100 ];fs=[1100 ,1900 ];end 8000 ; 1 ;Rs=40 ;2 *pi *fp;Ws=2 *pi *fs; 's' );switch filter_typecase 1 'low' ,'s' );case 2 'high' ,'s' );case 3 'bandpass' ,'s' );case 4 'stop' ,'s' );end abs (H);angle (H);20 *log10 ((mag+eps )/max (mag));2 *pi );2 ,1 ,1 );plot (f,db);'模拟滤波器幅频曲线' );xlabel('频率(Hz)' );ylabel('幅度(dB)' );0 fm -80 5 ]); 2 ,1 ,2 );plot (f,pha);'模拟滤波器相频曲线' );xlabel('频率(Hz)' );ylabel('相位(rad)' );0 fm -4 4 ]);
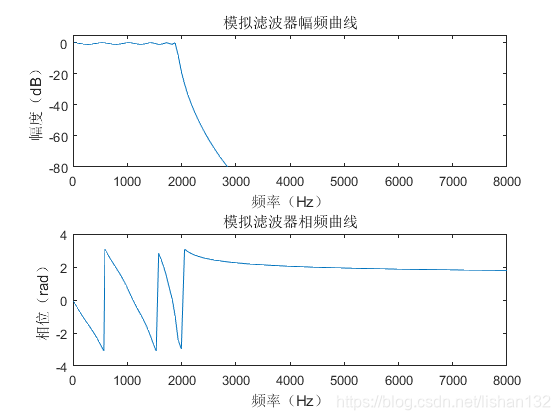
模拟低通切比雪夫1型滤波器设计效果如下
切比雪夫2型模拟滤波器
1、cheb2ord函数
[N,Wc]=cheb1ord(Wp,Ws,Rp,Rs,’s’);%计算切比雪夫2模拟滤波器参数,‘s’表示Wp和Ws都是模拟角频率
2、cheby2函数
[b,a]=cheby2(N,Rs,Wp,’low’,’s’);%设计切比雪夫2低通滤波器,其中的‘low’可以替换成’bandpass’、’high’、’stop’,分别表示带通、高通、带阻滤波器
Matlab程序设计如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 1900 ;fs=2200 ;1 ;Rs=40 ;12000 ; 1 ;2 *pi *fp;Ws=2 *pi *fs; 's' );switch filter_typecase 1 'low' ,'s' );case 2 'high' ,'s' );case 3 'bandpass' ,'s' );case 4 'stop' ,'s' );end abs (H);angle (H);20 *log10 ((mag+eps )/max (mag));2 *pi );2 ,1 ,1 );plot (f,db);'模拟滤波器幅频曲线' );xlabel('频率(Hz)' );ylabel('幅度(dB)' );0 fm -80 5 ]); 2 ,1 ,2 );plot (f,pha);'模拟滤波器相频曲线' );xlabel('频率(Hz)' );ylabel('相位(rad)' );0 fm -4 4 ]);
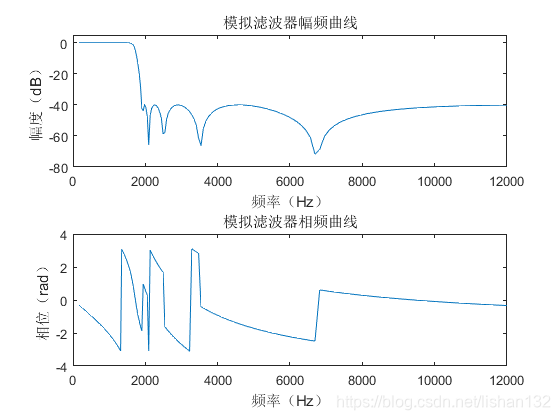
模拟低通切比雪夫2型滤波器设计效果如下
2.1.3 椭圆滤波器设计 椭圆滤波器幅频特性曲线如下
1、ellipord函数
[N,Wc]=ellipord(Wp,Ws,Rp,Rs,’s’);%计算椭圆模拟滤波器参数,‘s’表示Wp和Ws都是模拟角频率
2、ellip函数
[b,a]=ellip(N,Rp,Rs,Wp,’low’,’s’);%设计椭圆滤波器低通滤波器其中的‘low’可以替换成’bandpass’、’high’、’stop’,分别表示带通、高通、带阻滤波器
Matlab程序设计如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 1 ;switch filter_typecase 1 1900 ;fs=2200 ;case 2 5100 ;fs=4800 ;case 3 1100 ,1900 ];fs=[900 ,2100 ];case 4 900 ,2100 ];fs=[1100 ,1900 ];end 12000 ; 1 ;Rs=40 ;2 *pi *fp;Ws=2 *pi *fs; 's' );switch filter_typecase 1 'low' ,'s' );case 2 'high' ,'s' );case 3 'bandpass' ,'s' );case 4 'stop' ,'s' );end abs (H);angle (H);20 *log10 ((mag+eps )/max (mag));2 *pi );2 ,1 ,1 );plot (f,db);'模拟滤波器幅频曲线' );xlabel('频率(Hz)' );ylabel('幅度(dB)' );0 fm -80 5 ]); 2 ,1 ,2 );plot (f,pha);'模拟滤波器相频曲线' );xlabel('频率(Hz)' );ylabel('相位(rad)' );0 fm -4 4 ]);
模拟高通椭圆滤波器设计效果如下
2.2 模拟滤波器转数字滤波器 2.2.1 冲激响应不变法 冲激响应不变法:通过对模拟滤波器的单位冲激响应进行采样得到数字滤波器的单位冲激响应,也就是从S平面映射到Z平面。冲激响应不变法只能设计带限系统,即通过冲激响应不变法对低通、带通模拟滤波器离散时,必须附加适当的带限条件,这里的带限表示滤波器的工作有一个最大频率,只能在某个频率范围内设计滤波器。在模拟滤波器设计完后使用冲激响应不变法变为数字滤波器, 模拟滤波器的设计方法与上文步骤一样。
1 2 [B,A]=impinvar(b,a,Fs);
完整程序如下:
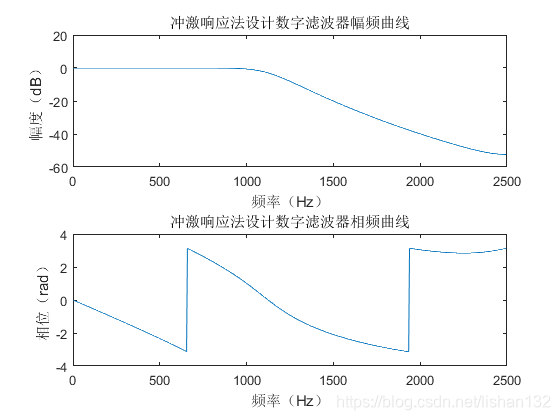
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 1 ;switch filter_typecase 1 1900 ;fs=2200 ;5000 ;case 2 6000 ;fs=4000 ;15000 ;case 3 1100 ,1900 ];fs=[900 ,2100 ];5000 ;case 4 900 ,2100 ];fs=[1100 ,1900 ];5000 ;end 1 ;Rs=40 ;2 *pi *fp;Ws=2 *pi *fs; 's' );switch filter_typecase 1 'low' ,'s' );case 2 'high' ,'s' );case 3 'bandpass' ,'s' );case 4 'stop' ,'s' );end abs (H);angle (H);20 *log10 ((mag+eps )/max (mag));2 *pi );2 ,1 ,1 );plot (f,db);'冲激响应法设计数字滤波器幅频曲线' );xlabel('频率(Hz)' );ylabel('幅度(dB)' );2 ,1 ,2 );plot (f,pha);'冲激响应法设计数字滤波器相频曲线' );xlabel('频率(Hz)' );ylabel('相位(rad)' );
冲激响应不变法设计数字低通滤波器效果如下
2.2.2 双线性映射法 冲激响应不变法的幅频特性存在混叠失真现象,这是因为从S平面到Z平面的变换出现了多值对应,为了克服多值对应带来的混叠失真,提出了双线性映射法。双线性映射法先将整个S平面(负无穷到正无穷)压缩到S1平面(-π/T,π/T),再将S1平面映射到Z平面。采用双线性映射法虽然改善了混叠失真现象,但是又带来了相位畸变失真,为此,需要在在设计模拟滤波器前进行反畸变。最后,在模拟滤波器设计完成后使用双线性映射法变为数字滤波器系统函数的参数。代码如下:
1 2 3 4 5 6 7 2 *pi *fp/Fs; ws=2 *pi *fs/Fs; 2 *Fs)*tan (wp/2 );Ws =(2 *Fs)*tan (ws/2 );
完整代码如下
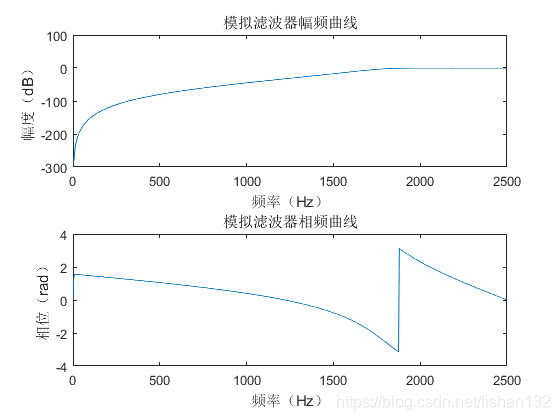
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 4 ;switch filter_typecase 1 1900 ;fs=2200 ;5000 ;case 2 6000 ;fs=4000 ;15000 ;case 3 1100 ,1900 ];fs=[900 ,2100 ];5000 ;case 4 900 ,2100 ];fs=[1100 ,1900 ];5000 ;end 1 ;Rs=40 ;2 *pi *fp/Fs; ws=2 *pi *fs/Fs; abs ((2 *Fs)*tan (wp/2 ));Ws =abs ((2 *Fs)*tan (ws/2 )); 's' );switch filter_typecase 1 'low' ,'s' );case 2 'high' ,'s' );case 3 'bandpass' ,'s' );case 4 'stop' ,'s' );end abs (H);angle (H);20 *log10 ((mag+eps )/max (mag));2 *pi );2 ,1 ,1 );plot (f,db);'双线性映射法设计数字滤波器幅频曲线' );xlabel('频率(Hz)' );ylabel('幅度(dB)' );2 ,1 ,2 );plot (f,pha);'双线性映射法设计数字滤波器相频曲线' );xlabel('频率(Hz)' );ylabel('相位(rad)' );
双线性映射法设计数字高通滤波器效果如下
2.3 直接设计数字滤波器 ①可以直接使用设计模拟滤波器时的函数,只不过函数参数中不再有‘s’,相应的频率参数也变为归一化频率。
1、[N,Wc]=buttord(Wp,Ws,Rp,Rs);没有参数‘s’时,表示生成巴特沃斯数字滤波器的参数,此时,Wp、Ws和Wc表示归一化的频率,1代表归一化的奈奎斯特采样频率。例如通带频率50Hz,阻带频率60Hz,采样频率500Hz,此时Wp=50/500Hz,Ws=60/500Hz
2、[b,a] = butter(N,Wc);没有参数‘s’时,返回具有归一化截止频率Wc的N阶低通数字巴特沃斯滤波器的传递函数系数。
3、[H,W]=freqz(b,a);%数字滤波器系统函数
②借助差分方程完成
假设参数a1=-1,a2=-1,b0=1,b1=1,b2=1
Matlab程序如下所示:
1 2 3 4 5 6 7 8 9 10 1 )=b(0 )*x(1 );2 )=b(0 )*x(2 )+b(1 )*x(1 )+a1*y(1 );for n=3 :length (x)0 )*x(n)+b(1 )*x(n-1 )+b(2 )*x(n-2 )+a(1 )*y(n-1 )+a(2 )*y(n-2 );end
3 FIR数字滤波器的设计方法 3.1 窗函数法 Matlab代码设计如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 2000 ;fs=1000 ;1 ;Rs=45 ;5000 ;2 ;2 *pi *fp/Fs; ws=2 *pi *fs/Fs; abs (wp-ws);2 ;ceil (P*4 *pi /tr_width);mod (N0+1 ,2 );-1 )/2 ;2 ;0 :1 :N-1 );eps ;sin (pi *nm)-sin (wc*nm))./(pi *nm);1 ,100 );abs (H);pha=angle (H);20 *log10 ((mag+eps )/max (mag));2 ,1 ,1 );plot (W*Fs/(2 *pi ),db);'窗函数设计FIR滤波器幅频曲线' );xlabel('频率(Hz)' );ylabel('幅度(dB)' );2 ,1 ,2 );plot (W*Fs/(2 *pi ),pha);'窗函数设计FIR滤波器相频曲线' );xlabel('频率(Hz)' );ylabel('相位(rad)' );
4 Matlab自动生成滤波器代码工具 在Matlab命令窗口输入fdatool即可打开Matlab自带的滤波器代码生成工具,其他更详细的使用说明请见doc Using FDAtool
更新:新版matlab已经将启动命令修改为filterDesigner
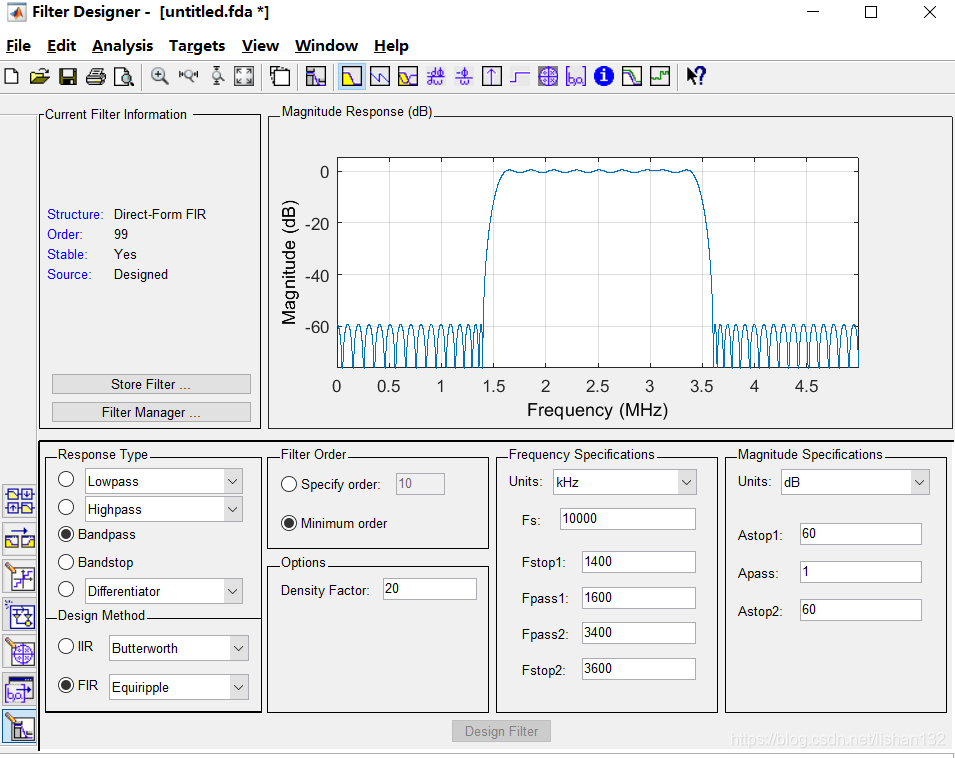
Matlab自带的滤波器代码生成工具界面如下
设置好滤波器各项参数后,点击设计界面下方的Design Filter按钮即可。然后依次点击File→Generate MATLAB Code→Filter Design Function,自动生成滤波器代码,并保存为.m脚本文件
图中参数设置如下:
响应类型:带通滤波器
设计模式:FIR
滤波器阶数:自动使用最小阶数
采样频率:10000KHz
阻带频率1:1400KHz
通带频率1:1600KHz
通带频率2:3400KHz
阻带频率2:3600KHz
阻带1衰减:60dB
通带衰减: 1dB
阻带2衰减:60dB
自动生成的Matlab代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 function Hd = Bandpass_FIR 10000 ; 1400 ; 1600 ; 3400 ; 3600 ; 0.001 ; 0.057501127785 ; 0.001 ; 20 ; 2 ), [0 1 ...0 ], [Dstop1 Dpass Dstop2]);
调用生成的滤波器代码格式为:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 abs (H); 20 *log10 (mag);angle (H); 1e4 /(2 *pi )/(1e3 ); 3 ,2 ,3 );plot (f2,db);'FIR滤波器幅频曲线' );'Frequency(MHz)' );ylabel('Amplitude(dB)' );3 ,2 ,4 );plot (f2,pha);'FIR滤波器相频曲线' );'Frequency(MHz)' );ylabel('Phase(rad)' );
5 数字滤波器的功能测试 数字滤波器设计完成之后,还要检查一下它的滤波效果如何。此时可以利用数字滤波器直接对一个输入信号进行滤波操作,观察滤波前后信号的频率成分有何变化。但是因为这个输入信号一般并没有将滤波器工作频带内的所有频率成分包括完,所以这个测试结果是不严谨的。更合适的做法是先生成一个扫频测试信号,随着时间的增加,信号的频率成分从某一点逐渐增加或减少到另一点,看起就像是将整个范围类内的频率成分扫描一遍,所以称为扫频。需要注意的是,因为计算机只能处理离散的数字,所以扫频信号包含的频率成分是离散变化的。根据频率变化的快慢,扫频信号有线性扫频,二次扫频、对数扫频几种,根据频率变化的趋势,有递增扫频、递减扫频;还可以根据自己需要,生成周期扫频信号。
Matlab中,扫描信号可使用chirp函数实现,在matlab命令窗口中输入doc chirp可查看详情,默认使用线性扫频方法
pspectrum函数可用于对信号进行时频分析,既考虑了时间分辨率的影响,也考虑了频率分辨率的作用
5.1 生成扫频信号 下面举例说明如何生成一个1MHz到5MHz的线性扫描信号
1、根据奈奎斯特采样定理,采样频率要大于信号最大频率的2倍,所以我们选择采样频率Fs为2×5MHz=10MHz,也就是10×10^6Hz。
2、采样的起始时间为0s,结束时间设为1ms。因采样频率太高(10MHz),采样间隔非常短(10ns),若采样总时间过长,采集的数据量太多,程序的运行会非常耗时,甚至会出现内存不足的情况,因此总时间设为1ms,即1×10^(-3)s。当然这个时间可以自行调整,不一定为1ms。
3、信号最小频率为1MHz,信号最大频率为5MHz。
4、生成采样时间点向量t,采样时间间隔为1/Fs=10ns,采样点数为(1ms-0)×10MHz=2000。可以看到,如果采样总时间过长,采集量就会成10^7的倍数增加,庞大的数据量会带来不必要的处理时间。如果采样的频率不高的话,可以选择增加采样总时长。
5、使用chirp函数生成扫频信号,不指明生成方法参数时(linear、quadratic、logarithmic),默认为线性扫频
x = chirp(t,min,Time_finish,max);第一个参数为采样时间点向量,第二个参数为起始频率,第三个参数为指定一个时间点,第四个参数为指定时间点的频率。也可以理解为指定两点,生成一条直线。
6、使用pspectrum对扫频信号进行时频分析,记得加上spectrogram参数,表示进行谱分析,若不加此参数,就只会显示功率谱曲线。TimeResolution为时间分辨率,FrequencyResolution为频率分辨率,两者只能指定其中一个值。
1 2 3 4 5 6 7 8 9 10 10e6 ; 0 ; 1e-3 ; min = 1e6 ; max = 5e6 ; 1 /Fs:Time_finish-1 /Fs; min ,Time_finish,max ); 'spectrogram' ,'TimeResolution' ,1 /Fs*100 ,'OverlapPercent' ,99 ,'Leakage' ,0.85 )
5.2 滤波处理 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 10e6 ; 0 ; 1e-3 ; min = 1e6 ; max = 5e6 ; 1 /Fs:Time_finish-1 /Fs; min ,Time_finish,max ); figure (1 )121 )'spectrogram' ,'TimeResolution' ,1 /Fs*100 ,'OverlapPercent' ,99 ,'Leakage' ,0.85 )figure (2 )3 ,2 ,1 );plot (t,x);'滤波前扫频信号时域图' );'Time(s)' );ylabel('Amplitude' );length (x);2 ^nextpow2 (L1);abs (Xk1); 20 *log10 (mag1); 0 :NFFT1/2 -1 ;1e6 ); 3 ,2 ,2 );plot (f1,db1(1 :NFFT1/2 ));'滤波前扫频信号频谱图' );'Frequency(MHz)' );ylabel('Amplitude(dB)' )abs (H); 20 *log10 (mag);angle (H); 1e4 /(2 *pi )/(1e3 ); 3 ,2 ,3 );plot (f2,db);'FIR滤波器幅频曲线' );'Frequency(MHz)' );ylabel('Amplitude(dB)' );3 ,2 ,4 );plot (f2,pha);'FIR滤波器相频曲线' );'Frequency(MHz)' );ylabel('Phase(rad)' );3 ,2 ,5 );plot (t,y);'滤波后扫频信号时域图' );'Time(s)' );ylabel('Amplitude' );length (y);2 ^nextpow2 (L3);abs (Xk3); 20 *log10 (mag3); 0 :NFFT3/2 -1 ;1e6 ); 3 ,2 ,6 );plot (f3,db3(1 :NFFT3/2 ));'滤波后扫频信号频谱图' );'Frequency(MHz)' );ylabel('Amplitude(dB)' )figure (1 )122 )'spectrogram' ,'TimeResolution' ,1 /Fs*100 ,'OverlapPercent' ,99 ,'Leakage' ,0.85 )
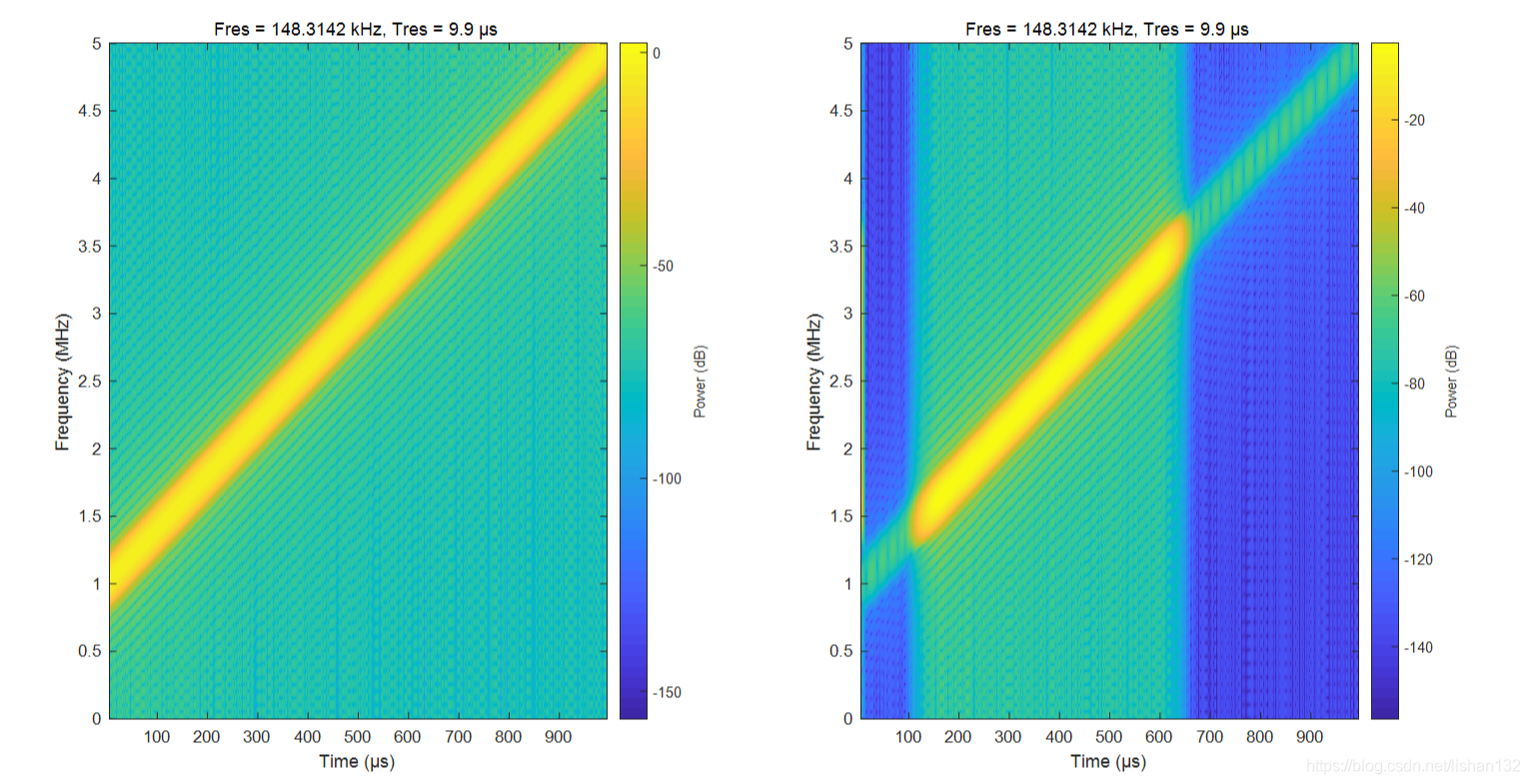
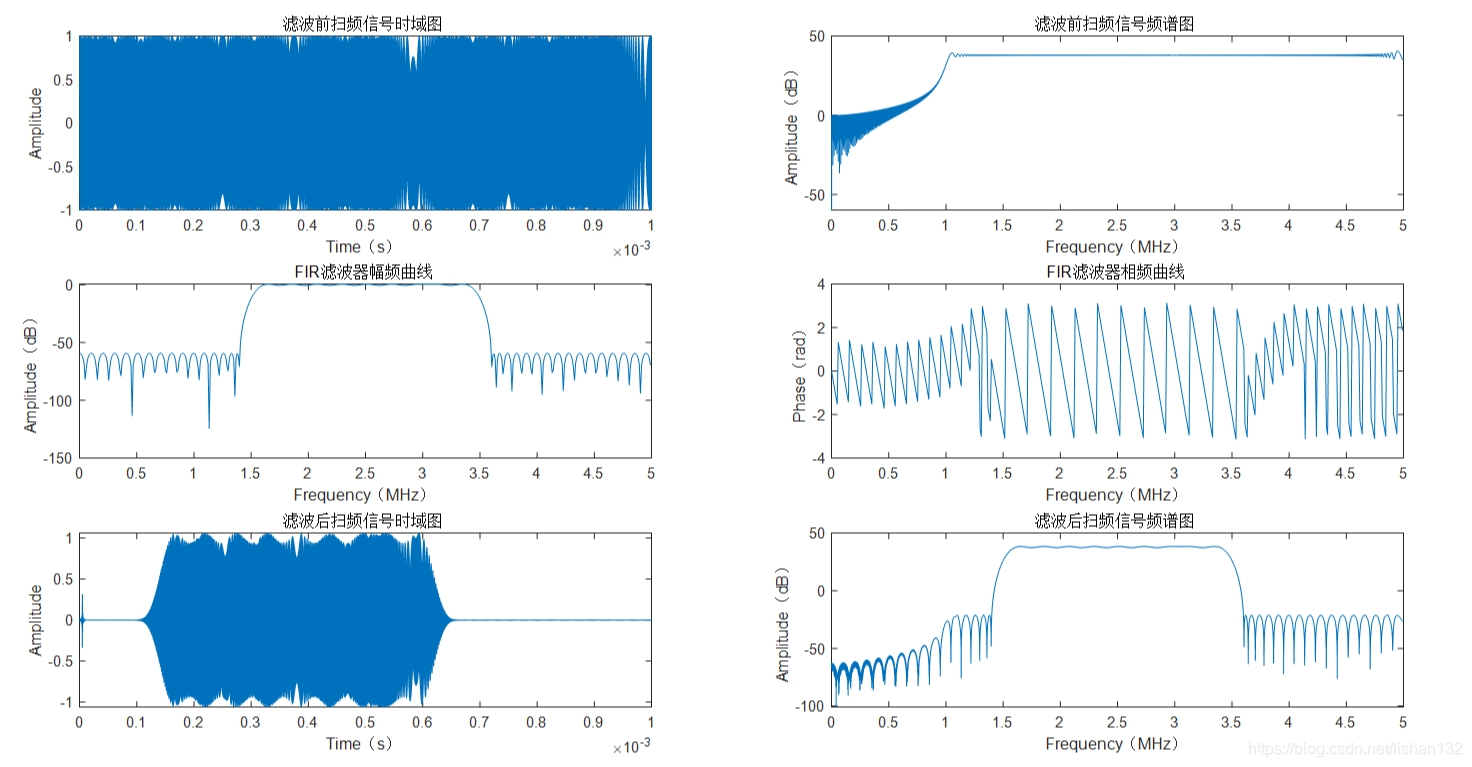
生成的FIR滤波器对扫频信号进行滤波效果测试如下
滤波前后扫频信号时频分析图如下
6 结语 无论是文字、图像、音频还是视频等信息,滤波器在这些信息的处理中起到了基础性的工作,DSP、FPGA等高端处理器中也经常使用数字滤波器算法,掌握滤波器的设计方法对于电子、通信、计算机领域的工作人员来说至关重要。本文仅仅总结了Matlab下最基本滤波器的设计方法,未来还会继续总结最新的数字滤波器算法和移植,以此勉励自己。
在Matlab软件中的主页 →帮助 →文档 ,选择Signal Processing Toolbox →Digital and Analog Filters 可以查看更多详细内容
2019年12月5日于西安工业大学
参考文献:
[1] Matlab官网数字和模拟滤波器帮助网页 https://ww2.mathworks.cn/help/signal/digital-and-analog-filters.html